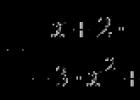Урок и презентация на тему: "Преобразование выражений, содержащих радикал"

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 11 класса
Интерактивное пособие для 9–11 классов "Тригонометрия"
Интерактивное пособие для 10–11 классов "Логарифмы"

Ребята, на прошлом уроке мы изучили свойства корня n-ой степени. Сегодня мы посмотрим, как их применять при решении различных задач которые могут встретиться на практике.

Давайте сделаем небольшую памятку из свойств наших корней:
1. ${(\sqrt[n]{a})}^n=a$; $\sqrt[n]{a^n}=a$.
2. $\sqrt[n]{a*b}=\sqrt[n]{a}*\sqrt[n]{b}$.
3. $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$, $b≠0$.
4. ${(\sqrt[n]{a})}^k=\sqrt[n]{a^k}$.
5. $\sqrt[n]{\sqrt[k]{a}}=\sqrt{a}$.
6. $\sqrt{a^{k*p}}=\sqrt[n]{a^{k}}$.

Используя наши формулы, мы можем преобразовывать выражения содержащие радикалы (операция извлечения корня), такие выражения называются иррациональными.

Пример.
Упростить выражение:
а) $\sqrt{48a^7}$.
б) ${(\sqrt{a^3})}^2$.
Решение.
а) Подкоренное выражение приведем к виду: $16*a^4*3a^3$.
Тогда, используя формулу 2 из нашей памятки, исходное выражение примет вид:
$\sqrt{48a^7}=\sqrt{16*a^4*3a^3}=\sqrt{16}*\sqrt{a^4}*\sqrt{3a^3}=2a*\sqrt{3a^3}$.
Полученное нами выражение считается более простым, так как под знаком корня более простое выражение.
Преобразование такого вида называется – вынесением множителя за знак радикала.

Б) Воспользуемся формулой 4: ${(\sqrt{a^3})}^2=\sqrt{{(a^3)}^2}=\sqrt{a^6}$.
Преобразуем полученное выражение тем же методом, что и в первом примере. $\sqrt{a^6}=\sqrt{a^5*a}=\sqrt{a^5}*\sqrt{a}=a*\sqrt{a}$.
При вынесении множителя за знак радикала следует обратить особое внимание на знак выносимого множителя. В случае четных степеней он может быть как положительным, так и отрицательным.

Давайте рассмотрим пример: $\sqrt{x^6*y}$.
О знаке числа х мы ничего не знаем, преобразовав наше выражение получим: $x*\sqrt{y}$.
На самом деле эта запись неверная. Повторимся: о знаке числа х мы ничего не знаем. Как быть в этом случае?
Для того чтобы быть уверенным, что ответ правильный, лучше представить его виде: $|x|*\sqrt{y}$.
Обобщенная формула для корней с четным показателем будет выглядеть так: $\sqrt{a^{2n}}=|a|$.

Ребята, мы рассмотрели операцию вынесение множителя за знак радикала. Существует и обратная операция – внесение множителя под знак радикала.

Пример.
Сравнить числа $4\sqrt{2}$ и $2\sqrt{4}$.
Решение.
Мы знаем: $4=\sqrt{64}$ и $2=\sqrt{8}$.
Преобразуем исходное выражение:
$4\sqrt{2}=\sqrt{64}*\sqrt{2}=\sqrt{128}$.
$2\sqrt{4}=\sqrt{8}*\sqrt{4}=\sqrt{32}$.
Показатели корней обоих выражений одинаковые. Больше то число, у которого больше подкоренное выражение. В нашем случае: $\sqrt{128}>\sqrt{32}$.

Пример.
Упростить выражение: $\sqrt{x^3*\sqrt{x}}$.
Решение.
Внесем выражение, содержащее третью степень, под знак корня:
$x^3*\sqrt{x}=\sqrtx^{12}*\sqrt{x}=\sqrt{x^{13}}$.
Воспользуемся формулой 5. Исходное выражение можно представить в виде: $\sqrt{\sqrt{x^{13}}}=\sqrt{x^{13}}$.

Пример.
Выполнить действия:
а) $(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})$.
б) $(\sqrt{a}-\sqrt{b})(\sqrt{a^2}+\sqrt{ab}+\sqrt{b^2})$.
Решение:
а) Воспользуемся формулой разности квадратов:
$(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})=(\sqrt{a^2}+\sqrt{b^2})$.
Теперь давайте упростим полученное нами выражение, воспользуемся формулой 6 нашей памятки:
$(\sqrt{a^2}-\sqrt{b^2})=(\sqrt{a}-\sqrt{b})$ (показатель корня и степень подкоренного выражения разделили на 2.
Ответ: $(\sqrt{a^2}-\sqrt{b^2})(\sqrt{a^2}+\sqrt{b^2})=(\sqrt{a}-\sqrt{b})$.

Б) Давайте внимательно посмотрим на наше выражение. Оно похоже на формулу разности кубов, давайте ее и применим:
$(\sqrt{a}-\sqrt{b})(\sqrt{a^2}+\sqrt{ab}+\sqrt{b^2})={(\sqrt{a})}^3-{(\sqrt{b})}^3=a-b$.

Пример.
Выполнить действия:
а) $\sqrt{a^5}*\sqrt{a^3}$.
б) $\sqrt{3-\sqrt{3}}*\sqrt{12+6\sqrt{3}}$.
Решение.
Перемножать можно только корни одной и той же степени. Давайте приведем наши выражения к одинаковому показателю корня.
$\sqrt{a^5}=\sqrt{a^{10}}$ (домножили на 2).
$\sqrt{a^3}=\sqrt{a^{9}}$ (домножили на 3).
$\sqrt{a^5}*\sqrt{a^3}=\sqrt{a^{10}}*\sqrt{a^9}=\sqrt{a^{19}}$.
Упростим получившиеся выражение:
$\sqrt{a^{19}}=\sqrt{a^{12}*a^7}=|a|*\sqrt{a^7}$.
Обратим внимание на то, что показатель корня наших выражений – четный. Это значит, что подкоренное выражение содержит только положительные числа, то есть $a≥0$, но тогда $|a|=a$.
Ответ: $\sqrt{a^5}*\sqrt{a^3}=a*\sqrt{a^7}$.

Б)Этот пример можно решить двумя способами. Давайте рассмотрим каждый из способов:
1 способ. Приведем первый множитель к 4-ой степени:
$\sqrt{3-\sqrt{3}}=\sqrt{{(3-\sqrt{3})}^2}=\sqrt{9-6\sqrt{3}+3}=\sqrt{12-6\sqrt{3}}$.
Перемножим радикалы:
$\sqrt{12-6\sqrt{3}}*\sqrt{12+6\sqrt{3}}=\sqrt{{(12-6\sqrt{3})}*(12+6\sqrt{3})}=\sqrt{144-36*3}=\sqrt{144-108}=\sqrt{36}=\sqrt{6^2}=\sqrt{6}$.

2 способ. Посмотрим на подкоренное выражение во втором множителе:
$12+6\sqrt{3}=9+6\sqrt{3}+3=3^2+2*3*\sqrt{3}+{(\sqrt{3})}^2={(3+\sqrt{3})}^2$.
Мы можем преобразовать множитель в целом:
$\sqrt{12+6\sqrt{3}}=\sqrt{{(3+\sqrt3)}^2}=\sqrt{3+\sqrt{3}}$ (разделили на 2 показатели степеней).
Преобразуем всё выражение:
$\sqrt{3-\sqrt{3}}*\sqrt{12+\sqrt{3}}=\sqrt{3-\sqrt{3}}*\sqrt{3+\sqrt{3}}=\sqrt{(3-\sqrt{3})*(3+\sqrt{3})}=\sqrt{9-3}=\sqrt{6}$.

Пример.
Разложить на множители выражение: $\sqrt{x^8}-2\sqrt{x^4y^2}+\sqrt{y^4}$.
Решение.
Перепишем исходное выражение в виде:
$\sqrt{x^8}-2\sqrt{x^4y^2}+\sqrt{y^4}={(\sqrt{x^4})}^2-2*\sqrt{x^4}*\sqrt{y^2}+{(\sqrt{y^2})}^2$ - это так называемый "квадрат разности".
$\sqrt{x^8}-2\sqrt{x^4y^2}+\sqrt{y^4}={(\sqrt{x^4}-\sqrt{y^2})}^2={(x\sqrt{x}-\sqrt{y^2})}^2$.

Пример.
Сократить дробь: $\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-2\sqrt{xy}+\sqrt{y}}$.
Решение.
1 способ.
Рассмотрим числитель и знаменатель отдельно:
$\sqrt{x}-\sqrt{y}=\sqrt{x^2}-\sqrt{y^2}=(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})$.
$\sqrt{x}-2\sqrt{xy}+\sqrt{y}=\sqrt{x^2}-2\sqrt{xy}+\sqrt{y^2}={(\sqrt{x}-\sqrt{y})}^2$.
Сократим получившиеся выражение:
$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-2\sqrt{xy}+\sqrt{y}}$=$\frac{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}{({\sqrt{x}-\sqrt{y})}^2}$=$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}-\sqrt{y}}$.

2 способ.
Введем замену переменных.
Пусть $a=\sqrt{x}$, $b=\sqrt{y}$. Тогда $\sqrt{x}=a^2$ и $\sqrt{y}=b^2$.
$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-2\sqrt{xy}+\sqrt{y}}=\frac{a^2-b^2}{{a^2-2ab+b}^2}=\frac{(a-b)(a+b)}{{(a-b)^2}}=\frac{(a+b)}{(a-b)}=\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}-\sqrt{y}}$.
Замена переменных часто упрощает ход решения. Работать с рациональными выражениями гораздо проще и привычней, чем с иррациональными.

Задачи для самостоятельного решения

1. Упростить выражение:
а) $\sqrt{162a^5}$.
б) ${(\sqrt{a^5})}^3$.
2. Сравнить числа: $3\sqrt{4}$ и $2\sqrt{5}$.
3. Упростить выражение: $\sqrt{{x^2}*\sqrt{x^2}}$.
4. Выполнить действия:
а) $\sqrt{a^7}*\sqrt{a^4}$.
б) $\sqrt{4-\sqrt{3}}*\sqrt{19+8\sqrt{3}}$.
5. Разложить на множители выражение: $\sqrt{x^6}-6\sqrt{x^3y^5}+9\sqrt{y^{10}}$.
6. Сократить дробь: $\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+2\sqrt{xy}+\sqrt{y}}$.

Свойства корней лежат в основе двух следующих преобразований, называемых внесением под знак корня и вынесением из-под знака корня, к рассмотрению которых мы и переходим.

Внесение множителя под знак корня

Внесение множителя под знак подразумевает замену выражения , где B и C – некоторые числа или выражения, а n – натуральное число, большее единицы, тождественно равным выражением, имеющим вид или .

Например, иррациональное выражение после внесения множителя 2 под знак корня принимает вид .

Теоретические основы этого преобразования, правила его проведения, а также решения всевозможных характерных примеров даны в статье внесение множителя под знак корня .

Вынесение множителя из-под знака корня

Преобразованием, в известном смысле обратным внесению множителя под знак корня, является вынесение множителя из-под знака корня. Оно состоит в представлении корня в виде произведения при нечетных n или в виде произведения при четных n , где B и C – некоторые числа или выражения.

За примером вернемся в предыдущий пункт: иррациональное выражение после вынесения множителя из-под знака корня принимает вид . Другой пример: вынесение множителя из-под знака корня в выражении дает произведение , которое можно переписать в виде .

На чем базируется это преобразование, и по каким правилам оно проводится, разберем в отдельной статье вынесение множителя из-под знака корня . Там же приведем решения примеров и перечислим способы приведения подкоренного выражения к виду, удобному для вынесения множителя.

Преобразование дробей, содержащих корни

Иррациональные выражения могут содержать дроби, в числителе и знаменателе которых присутствуют корни. С такими дробями можно проводить любые из основных тождественных преобразований дробей .

Во-первых, ничто не мешает работать с выражениями в числителе и знаменателе. В качестве примера рассмотрим дробь . Иррациональное выражение в числителе, очевидно, тождественно равно , а, обратившись к свойствам корней, выражение в знаменателе можно заменить корнем . В результате исходная дробь преобразуется к виду .

Во-вторых, можно изменить знак перед дробью, изменив знак числителя или знаменателя. Например, имеют место такие преобразования иррационального выражения: .

В-третьих, иногда возможно и целесообразно провести сокращение дроби. К примеру, как отказать себе в удовольствии сократить дробь на иррациональное выражение , в результате получаем .

Понятно, что во многих случаях, прежде чем выполнить сокращение дроби, выражения в ее числителе и знаменателе приходится раскладывать на множители, чего в простых случаях позволяют добиться формулы сокращенного умножения. А иногда сократить дробь помогает замена переменной, позволяющая от исходной дроби с иррациональностью перейти к рациональной дроби, работать с которой комфортнее и привычнее.

Для примера возьмем выражение . Введем новые переменные и , в этих переменных исходное выражение имеет вид . Выполнив в числителе

Класс: 8

Цели урока:

Учебная:

1. Углубить знания учащихся по теме квадратные корни и обобщить учебный материал.
2. Познакомить учащихся с понятием двойного радикала.
3. Научить преобразовывать двойные радикалы выделением полного квадрата подкоренного выражения.
4. Научить учащихся использовать формулу двойного радикала.
5. Развивать умения и навыки работы с иррациональными выражениями.

Развивающая :

1. Развитие внимания учащихся.
2. Развитие умения добиваться результатов труда.
3. Развитие интереса к изучению алгебры и навыков самостоятельной работы.

Воспитывающая:

1. Воспитание чувства коллективизма.
2. Формирование чувства ответственности за результат работы.
3. Формирование у учащихся адекватной самооценки при выборе отметки за работу на уроке.

Оборудование: компьютер, проектор.

Ход урока

1 этап работы. Организационный момент.

2 этап работы. Мотивация и выход на постановку проблемы

До восьмого класса мы осуществляли над числами пять арифметических действий: сложение, вычитание, умножение, деление и возведение в степень, причем при вычислениях, мы активно использовали различные свойства этих операций.

В курсе алгебры восьмого класса была введена новая операция – извлечение квадратного корня из неотрицательного числа. Выражения, содержащие операцию извлечения квадратного корня, называются иррациональными.

В большом толковом словаре можно найти следующее определение иррациональности:

С философской точки зрения иррациональность – недоступность разуму, то, что не может быть постигнуто разумом, что явно не подчиняется законам логики, и не может быть выражено в логических понятиях, что оценивается как «сверхразумное». С математической точки зрения иррациональность – несоизмеримость с единицей; не является ни целой, ни дробной величиной.

Действительно ли понятие иррациональности – это что-то «уму не постижимое, несоизмеримое, немыслимое»?

На этот вопрос мы постараемся сегодня найти ответ.

3 этап работы. Повторение ранее изученного материала

1) Свойства квадратного корня

Чтобы успешно выполнять преобразования выражений, содержащих операцию извлечения квадратного корня, нужно знать свойства этой операции.

Вспомним эти свойства:

1) Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел.

2) Если a≥0, b>0, то справедливо равенство

3) Если a≥0 и n – натуральное число, то

4) При любом a справедливо тождество

Если хорошо знать приёмы преобразования рациональных выражений, приёмы преобразования алгебраических дробей, усвоить определение понятия корня и свойства квадратного корня, уметь вносить множитель под знак квадратного корня, выносить множитель из – под знака квадратного корня, то можно выполнить преобразование любого выражения, содержащего операцию извлечения квадратного корня.

2) Способы преобразования радикалов

Кроме перечисленных теорем при преобразовании радикалов применяются некоторые специальные приёмы, тоже вытекающие из этих теорем, но требующие некоторого навыка.

Первый называется уничтожением иррациональности в знаменателе дроби. Если в знаменателе дроби имеется корень или несколько корней, то обращаться с такой дробью не совсем удобно. Смысл этого приёма заключается в том, что надо подобрать такой множитель, чтобы его произведение на знаменатель не содержало корней.

Второе интересное преобразование радикалов называется преобразованием двойного радикала.

4 этап работы. Ввести понятие двойного радикала и доказатьформулу сложного радикала.

Выражения вида и называют двойными радикалами или сложными радикалами. Преобразовать двойной радикалэто значит избавиться от внешнего радикала.

Справедливы тождества

При каждое подкоренное выражение неотрицательно.

Докажем эти равенства(доказывает ученик):

Для этого возведём в квадрат обе части данных выражений, воспользовавшись при этом формулой квадрата суммы (разности) двух чисел и формулой разности квадратов.

Возведем в квадрат левую часть:

Возведем в квадрат правую часть:

= ∙ = = = = = = =

Заметим, что доказанное тождество позволяет существенно облегчить вычисления и преобразования, если выражение представляет полный квадрат.

5 этап работы. Рассмотрим способы преобразования двойного радикала.

1 способ:

Можно выполнить алгебраические действия в некотором выражении, содержащем двойные радикалы.

Примеры:

= = = = = =

= = = = = =

= = = = = =

2 способ

Можно привести подкоренное выражение к полному квадрату.

Примеры:

Таким образом, если подкоренное выражение представить в виде полного квадрата, то можно легко освободиться от внешнего радикала.

Попробуем решить

НЕ УДАЕТСЯ!!!

3 способ

В тех случаях, когда подкоренное выражение нелегко представить в виде полного квадрата, то можно использовать готовую формулу сложного радикала

Примеры:

6 этап работы. Закрепление изученного материала.

Преобразуйте выражения, содержащие двойные радикалы:

7 этап работы. Вывод урока.

Преобразовать двойные радикалы можно следующим образом:

1. выполняя в выражении, содержащем двойные радикалы, алгебраические действия, применив свойства квадратных корней;
2. приводя подкоренное выражение к полному квадрату;
3. используя формулы сложного радикала.

8 этап работы. Домашнее задание.

Дома вы преобразуете двойные радикалы разными способами (раздать листы с заданиями).

Урок окончен. Спасибо за урок!

Алгебраические выражения, в записи которых используются не только четыре рациональных действия, но также знаки радикала (из буквенных выражений), мы называем иррациональными алгебраическими выражениями.

Таковы, например, выражения

При определении о. д. з. иррациональных алгебраических выражений следует учитывать, что выражения, находящиеся под знаком радикала четной степени, не должны быть отрицательными, При отыскании числовых значений выражения при данных буквенных значениях параметров корни четной степени понимаются в арифметическом смысле.

Пример 1. Найти о. д. з. выражения

и его значение при .

Решение. О. д. з. определяем из условий . Находим, что о. д. з. определяется неравенствами . При вычислении значения в заданной точке получаем

При преобразовании иррациональных алгебраических выражений используются все правила действий с корнями (гл. I, § 2). Рассмотрим сначала возможные упрощения выражения типа «корень из одночлена» или «корень из частного двух одночленов». Будем говорить, что корень приведен к простейшей форме, если: 1) он не содержит иррациональности в знаменателе, 2) в нем нельзя сократить его показатель с показателем подкоренного выражения и, наконец, 3) все возможные множители вынесены из-под корня. Всякий данный корень может быть приведен к простейшей форме, т. е. заменен тождественно равным ему, но таким, который отвечает всем трем перечисленным условиям.

Пример 2. Привести к простейшей форме следующие корни :

Решение, а) Сокращаем на 3 показатель корня и показатель степеней каждого из сомножителей подкоренного выражения

Выносим из-под знака корня множители а и ;

Корни, простейшие формы которых отличаются, быть может, лишь коэффициентами (числовыми или буквенными), принято называть подобными. Например, корни и подобны, так как а корни не подобны, так как

При сложении и вычитании подобных корней все они приводятся к простейшей форме, а затем корень выносится за скобки.

Пример 3. Произвести указанные действия:

Решение. Приведем каждый из корней к простейшей форме:

Теперь находим (все корни оказались подобными)

При вынесении сомножителей из-под знака корня четной степени необходимо помнить, что корень понимается в арифметическом смысле. Так, если знаки а, b не указаны, то следует писать не . Здесь о. д. з. состоит не только из значений , но и из значений а

Пример 4. Упростить выражение

Возможны следующие случаи:

Если не предполагать заранее, что , то решение примера еще усложнится, так как придется записать ответ в общей форме:

и затем разбирать четыре возможных случая: . Предоставляем завершить этот разбор читателю.

В примере, который мы сейчас решали, подкоренные выражения представлялись как точные квадраты некоторых двухчленов очевидным способом. В некоторых случаях такое представление подкоренного выражения производится не столь очевидным образом. Так, иногда можно упростить радикалы вида

Похожие статьи